Category Archives: Stata

Quy trình 13 bước chạy luận văn dữ liệu bảng panel bằng Stata

Stata

Nhóm MBA Bách Khoa giới thiệu đến bạn quy trình 13 bước chạy luận văn dữ liệu bảng panel bằng Stata. Luận văn thạc sĩ định lượng Stata trong bài này thuộc dạng định lượng, dữ liệu có được thông qua số liệu thứ cấp như là các chỉ số kinh tế vĩ mô, GDP, ROA, ROE…  Phân tích dữ liệu bảng panel là một kỹ thuật phổ biến trong các nghiên cứu kinh tế, đặc biệt là việc làm các đề tài luận văn định lượng về tài chính, chứng khoán, ngân hàng… giúp kiểm tra mối quan hệ giữa các biến qua thời gian.

Dưới đây là quy trình chi tiết 13 bước để chạy luận văn dữ liệu bảng panel bằng phần mềm Stata.

1. Lập mô hình nghiên cứu

Để bắt đầu, cần xác định rõ ràng câu hỏi nghiên cứu của đề tài và các giả thuyết cần kiểm tra.

Ví dụ tên đề tài là: Các yếu tố tác động đến tỷ suất sinh lợi của các ngân hàng TMCP tại Việt Nam

Mô hình nghiên cứu bao gồm xác định 1 biến phụ thuộc và các biến độc lập. Ví dụ, nếu bạn đang nghiên cứu Các yếu tố tác động đến tỷ suất sinh lợi của các ngân hàng TMCP tại Việt Nam, biến phụ thuộc  là Tỷ suất sinh lợi của các ngân hàng TMCP tại Việt Nam, trong khi các biến độc lập là: quy mô của ngân hàng, dư nợ cho vay khách hàng của ngân hàng,quy mô vốn chủ sở hữu của ngân hàng….
Một khi mô hình đã được xác định, cần viết ra dưới dạng một phương trình toán học, và các biến độc lập và phụ thuộc được định nghĩa như sau:

2. Thu thập số liệu thứ cấp

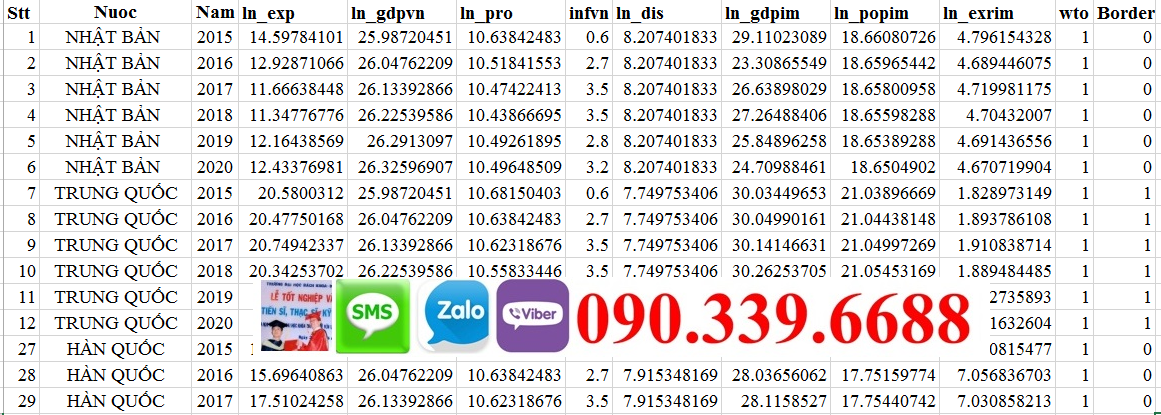
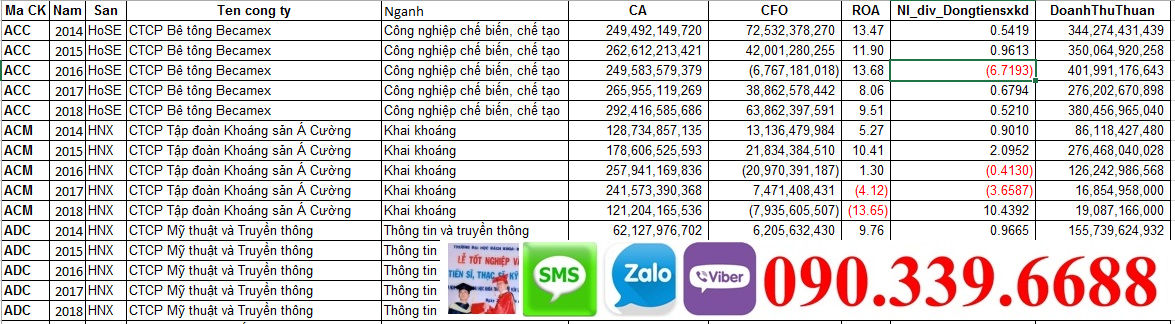
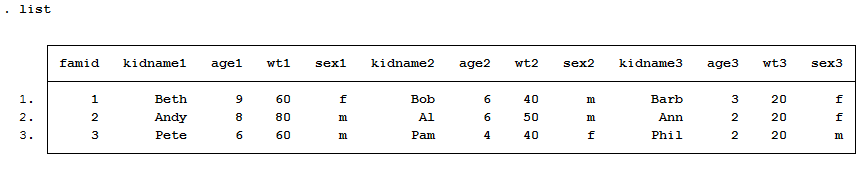
Thu thập dữ liệu là bước quan trọng tiếp theo. Dữ liệu bảng panel bao gồm dữ liệu theo dõi các đối tượng nghiên cứu qua nhiều thời gian. Ví dụ, dữ liệu có thể đến từ các cuộc điều tra hàng năm của các tổ chức chính phủ hoặc công ty chứng khoán, dữ liệu từ các cơ sở dữ liệu công cộng như World Bank, IMF, hoặc các báo cáo tài chính của công ty( thường thấy mọi người lấy ở vietstock )
Quan trọng là dữ liệu phải đầy đủ, chính xác và có độ tin cậy cao. Bạn cần kiểm tra tính nhất quán về đơn vị đo lường và sự thiếu sót trong dữ liệu trước khi sử dụng cho phân tích.

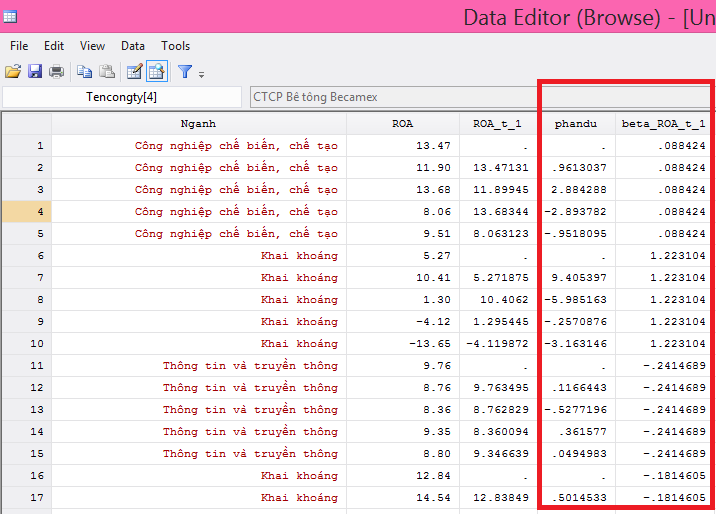
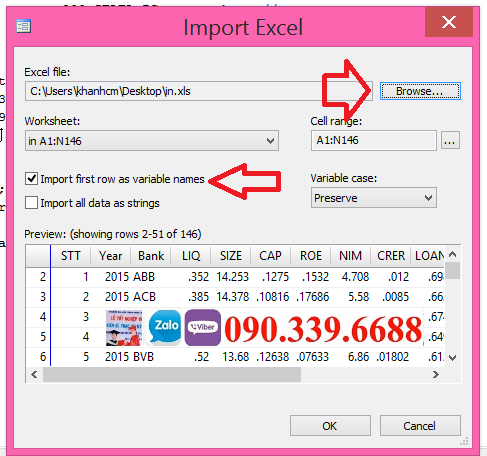
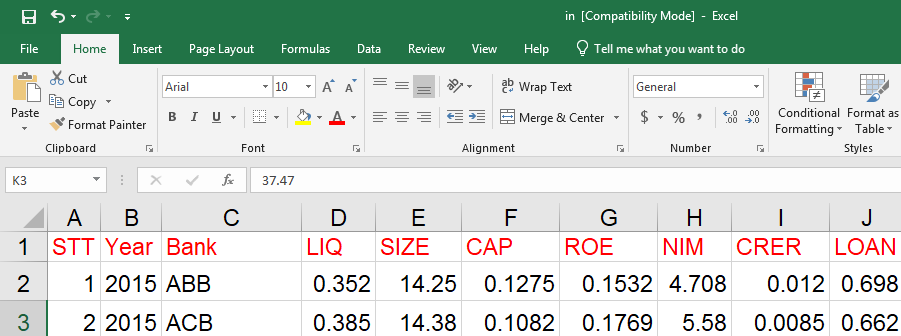
3. Đưa số liệu từ Excel vào Stata

Sau khi thu thập và làm sạch dữ liệu, bạn cần nhập chúng vào Stata. Để làm điều này, trước hết, lưu dữ liệu trong Excel dưới định dạng .xlsx. Sử dụng lệnh "import excel" để nhập dữ liệu vào Stata:
import excel " ", sheet("") firstrow
Lệnh trên sẽ nhập dữ liệu từ excel và hàng đầu tiên là tên các biến.

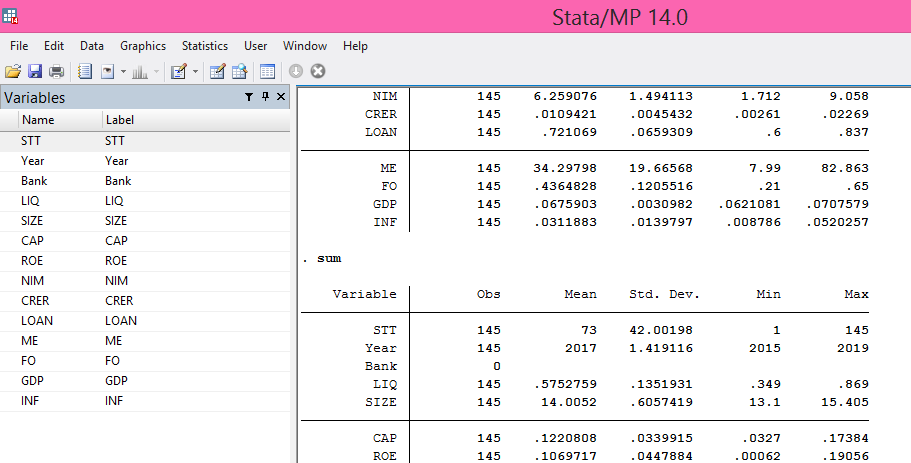
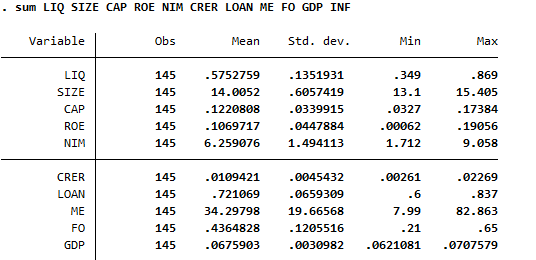
4. Chạy thống kê mô tả


Trước khi tiến hành phân tích sâu, chạy thống kê mô tả giúp ta hiểu rõ hơn về đặc điểm cơ bản của dữ liệu. Thống kê mô tả bao gồm các giá trị trung bình, độ lệch chuẩn, giá trị lớn nhất và nhỏ nhất, cũng như số lượng quan sát của mỗi biến.
Lệnh "summarize" trong Stata sẽ cung cấp một bản tóm tắt các đặc điểm chính của dữ liệu.  

5. Chạy tương quan

Phân tích tương quan giúp xác định mối quan hệ tuyến tính giữa các biến. Ma trận tương quan sẽ cho thấy mức độ và chiều hướng của mối quan hệ giữa các biến. Tương quan có thể dao động từ -1 đến 1,  giá trị càng gần 1 hoặc -1 chỉ ra mối quan hệ mạnh giữa cặp biến đó

correlate bien1 bien2 bien3

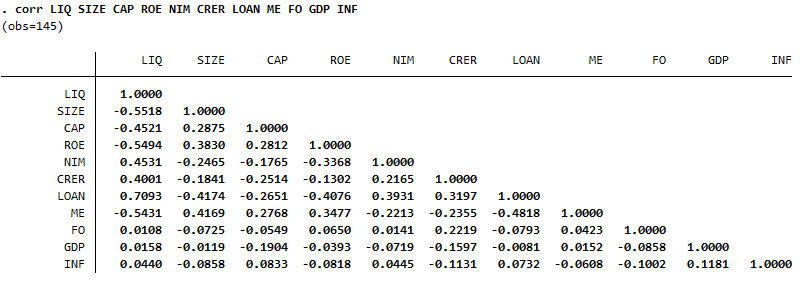
Việc này giúp ta phát hiện các mối quan hệ bất thường hoặc mạnh mẽ giữa các biến, từ đó có thể điều chỉnh mô hình cho phù hợp hơn, vì nếu các biến độc lập quan hệ với nhau quá mạnh có thể sinh ra đa cộng tuyến.

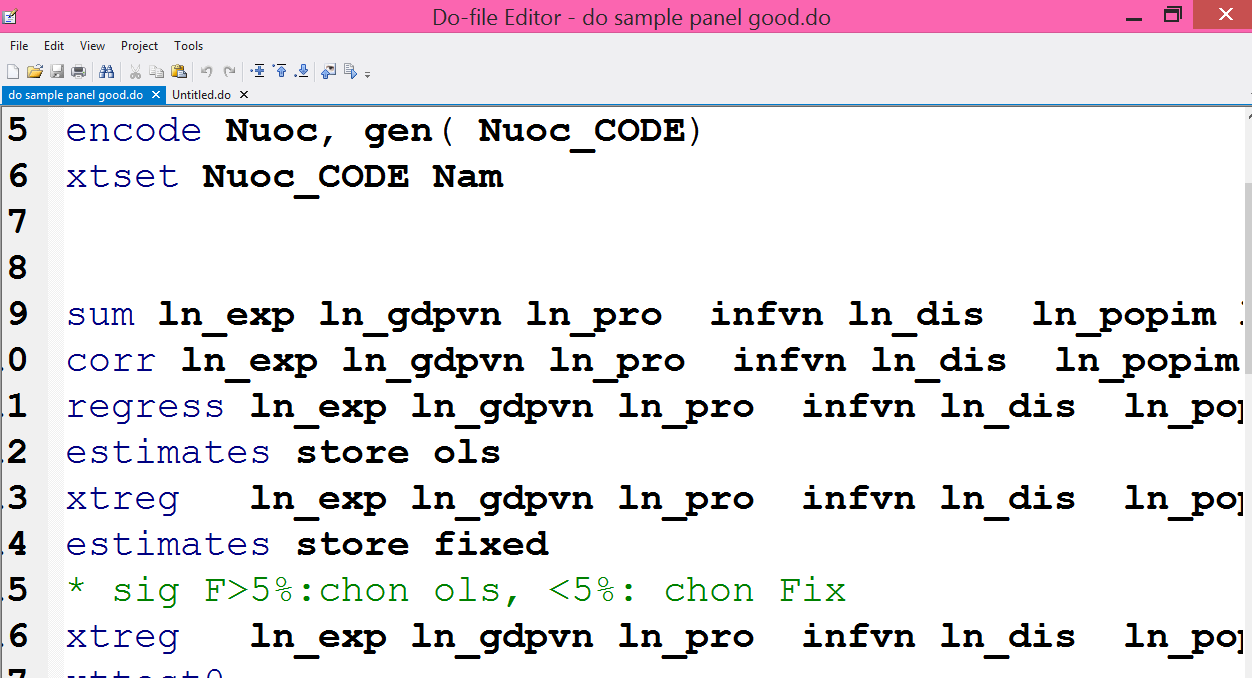
6. Chạy hồi quy OLS

Hồi quy OLS (Ordinary Least Squares) là phương pháp cơ bản để ước lượng mối quan hệ giữa biến phụ thuộc và các biến độc lập.  
regress bien_phu_thuoc bien_doc_lap1 bien_doc_lap2


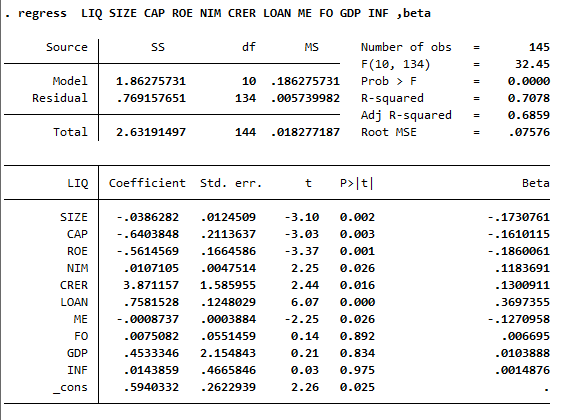
Lệnh "regress" trong Stata sẽ cho ta biết các hệ số hồi quy, giá trị p, và các chỉ số thống kê khác. Tuy nhiên, OLS không thể kiểm soát hiệu ứng theo không gian hoặc thời gian, do đó kết quả có thể bị thiên lệch nếu có sự khác biệt không quan sát được giữa các đối tượng theo không gian hoặc thời gian.

7. Chạy hồi quy hiệu ứng cố định

Hồi quy hiệu ứng cố định (Fixed Effects) giúp kiểm soát các yếu tố không quan sát được mà có thể khác nhau giữa các đối tượng nhưng không thay đổi theo thời gian.  
xtreg bien_phu_thuoc bien_doc_lap1 bien_doc_lap2, fe


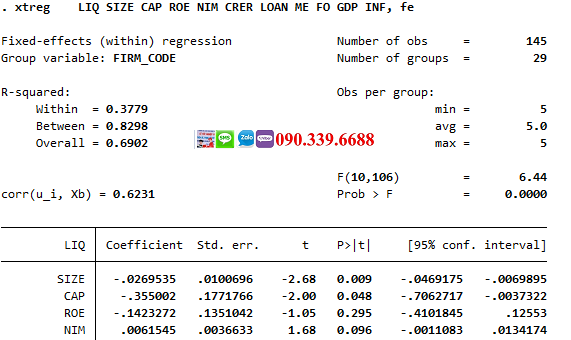
Lệnh "xtreg" với tùy chọn "fe" trong Stata sẽ loại bỏ các biến không thay đổi theo thời gian bằng cách chuyển đổi dữ liệu. Mô hình này giả định rằng các đặc điểm không quan sát được của các đơn vị nghiên cứu là khác nhau nhưng cố định trong suốt khoảng thời gian nghiên cứu.

8. Chạy hồi quy hiệu ứng ngẫu nhiên

Hồi quy hiệu ứng ngẫu nhiên (Random Effects) giả định rằng các yếu tố không quan sát được là ngẫu nhiên và không có tương quan với các biến độc lập. Điều này cho phép các biến không thay đổi theo thời gian vẫn có thể tham gia vào mô hình.
xtreg bien_phu_thuoc bien_doc_lap1 bien_doc_lap2, re


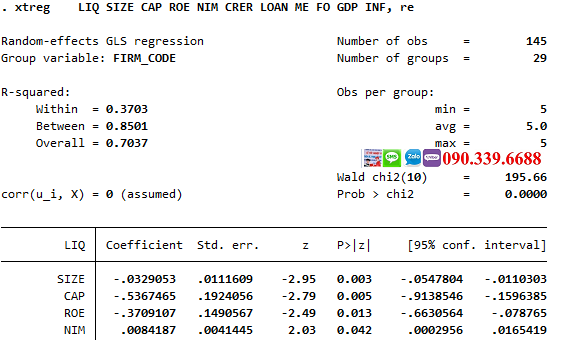
Lệnh "xtreg" với tùy chọn "re" trong Stata sẽ thực hiện hồi quy hiệu ứng ngẫu nhiên, giúp ước lượng các hệ số hồi quy với giả định rằng các sai số ngẫu nhiên là không tương quan với các biến độc lập.

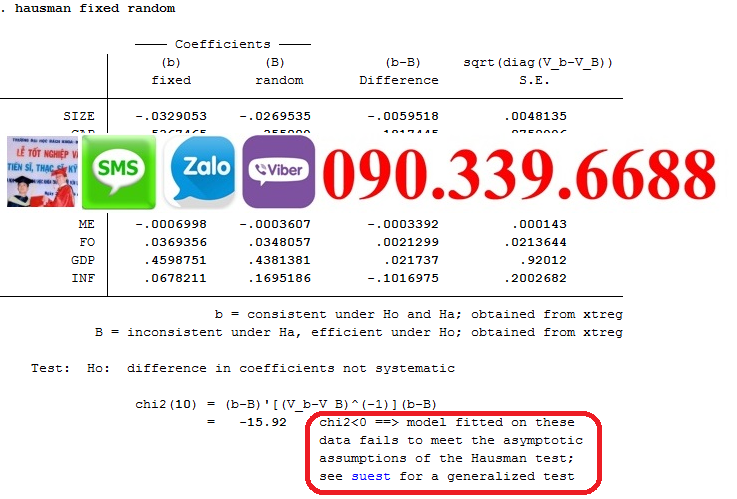
9. Kiểm định Hausman để chọn mô hình

Để xác định xem mô hình hiệu ứng cố định hay ngẫu nhiên là phù hợp hơn, bạn cần thực hiện kiểm định Hausman. Kiểm định này so sánh các ước lượng của hai mô hình và kiểm tra xem sự khác biệt có ý nghĩa thống kê hay không.


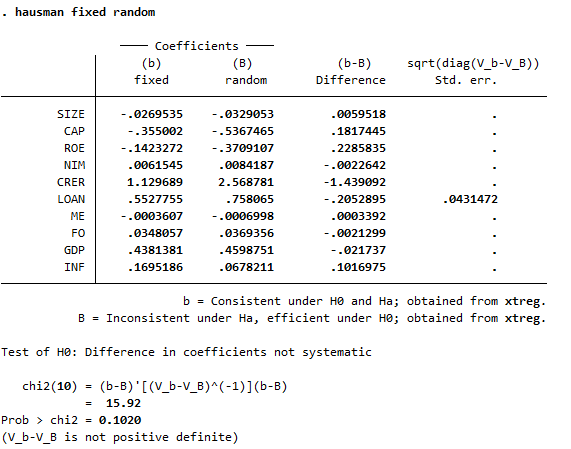
hausman fixed random
Nếu giá trị p của kiểm định Hausman nhỏ hơn 0.05, bạn sẽ chọn mô hình hiệu ứng cố định, vì nó cho thấy rằng các ước lượng của hiệu ứng cố định và ngẫu nhiên khác nhau có ý nghĩa, nghĩa là giả định của mô hình hiệu ứng ngẫu nhiên không đúng.

10. Đánh giá đa cộng tuyến

Đa cộng tuyến xảy ra khi các biến độc lập có mối quan hệ tuyến tính mạnh mẽ với nhau, gây khó khăn cho việc ước lượng chính xác các hệ số hồi quy. Ta có thể kiểm tra đa cộng tuyến bằng cách tính hệ số phóng đại phương sai (VIF – Variance Inflation Factor).


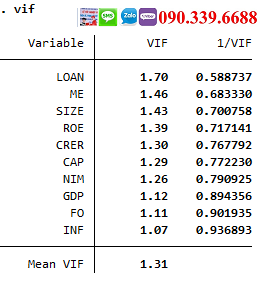
Nếu VIF của một biến lớn hơn 10, điều này có thể chỉ ra rằng biến đó có vấn đề về đa cộng tuyến và cần được xử lý, chẳng hạn như bằng cách loại bỏ biến hoặc kết hợp các biến lại với nhau.

11. Đánh giá phương sai thay đổi

Phương sai thay đổi (Heteroskedasticity) là hiện tượng mà phương sai của sai số thay đổi theo giá trị của các biến độc lập. Điều này có thể làm sai lệch các ước lượng hồi quy. Để kiểm tra hiện tượng này trong dữ liệu bảng panel, ta có thể sử dụng lệnh "xttest0" hoặc "xttest3" trong Stata.


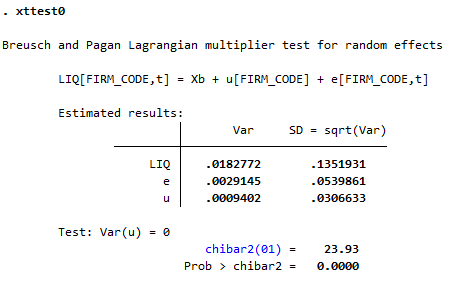
Lệnh "xttest0" hoặc "xttest3" trong Stata được sử dụng để kiểm định phương sai thay đổi trong mô hình hồi quy hiệu ứng cố định hoặc ngẫu nhiên. Lệnh này sẽ giúp bạn phát hiện xem có tồn tại phương sai thay đổi trong dữ liệu của mình hay không.
Kết quả của kiểm định sẽ cho biết liệu có tồn tại phương sai thay đổi trong mô hình hay không. Nếu giá trị p của kiểm định nhỏ hơn mức ý nghĩa  0.05, thì bạn có thể kết luận rằng có hiện tượng phương sai thay đổi. Và bạn cần phải khắc phục vấn đề này.
Nếu bạn phát hiện ra rằng có phương sai thay đổi, bạn có thể sử dụng các phương pháp như ước lượng sai số chuẩn mạnh (robust standard errors) hoặc hồi quy bình phương tổng quát (GLS) để khắc phục

12. Đánh giá tự tương quan

Tự tương quan (Autocorrelation) xảy ra khi các sai số hồi quy có tương quan với nhau qua thời gian, điều này thường gặp trong dữ liệu bảng panel. Kiểm định Wooldridge giúp phát hiện tự tương quan trong dữ liệu bảng panel.

Nếu xtserial cho ra kiểm định Wooldridge cho thấy có tự tương quan, bạn cần thực hiện các biện pháp để khắc phục như bên dưới.

13. Khắc phục phương sai thay đổi, tự tương quan nếu có bằng GLS

Nếu phát hiện có phương sai thay đổi hoặc tự tương quan, bạn có thể sử dụng hồi quy bình phương tổng quát (GLS – Generalized Least Squares) để khắc phục. GLS cho phép xử lý dữ liệu có cấu trúc sai số phức tạp, đảm bảo các ước lượng hồi quy là chính xác hơn.


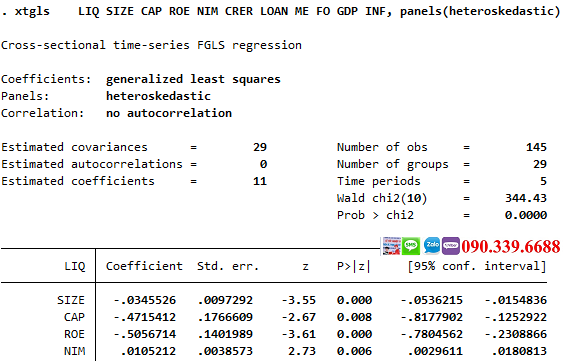
xtgls bien_phu_thuoc bien_doc_lap1 bien_doc_lap2, panels(correlated)
Lệnh "xtgls" sẽ thực hiện hồi quy GLS, giúp bạn xử lý các vấn đề về phương sai thay đổi và tự tương quan, từ đó cung cấp các ước lượng hồi quy chính xác hơn.

Trên đây là quy trình 13 bước chạy luận văn dữ liệu bảng panel bằng Stata. Việc thực hiện đúng các bước này sẽ giúp ta phân tích dữ liệu một cách hiệu quả và đạt được kết quả nghiên cứu chính xác.

Như vậy các bạn có thể hiểu rõ hơn về quy trình, các bước cần chạy trong bài luận văn định lượng của mình. Các bạn có thắc mắc hoặc cần trao đổi hỗ trợ cứ liên hệ nhóm nhé

Mô hình trọng lực ứng dụng và thực hành

Stata

Mô hình trọng lực là gì?

Mô hình trọng lực của thương mại quốc tế trong kinh tế quốc tế là một mô hình dự đoán dòng chảy thương mại song phương dựa trên quy mô kinh tế và khoảng cách giữa hai đơn vị( thường là 2 quốc gia). Thường giá trị thương mại có xu hướng giảm theo khoảng cách giữa hai quốc gia

Mô hình này được Walter Isard giới thiệu lần đầu tiên vào năm 1954. Mô hình cơ bản về thương mại giữa hai quốc gia ( i và j ) có dạng:

  • G là một hằng số
  • F là dòng chảy thương mại
  • D là khoảng cách
  • M là các khía cạnh kinh tế của các quốc gia đang được đo lường

Phương trình có thể được thay đổi thành dạng tuyến tính nhằm mục đích phân tích kinh tế lượng bằng cách sử dụng logarit. Mô hình này đã được các nhà kinh tế sử dụng để phân tích các yếu tố quyết định dòng chảy thương mại song phương như biên giới chung, ngôn ngữ chung, hệ thống pháp lý chung, tiền tệ chung, di sản thuộc địa chung và được sử dụng để kiểm tra tính hiệu quả của các hiệp định thương mại và các tổ chức như Hiệp định Thương mại Tự do Bắc Mỹ (NAFTA) và Tổ chức Thương mại Thế giới (WHO).

Mô hình trọng lực Tinbergen (1962) và Poyhonen (1963) là những nhà nghiên cứu đầu tiên ứng dụng mô hình trọng lực trong phân tích các yếu tố ảnh hưởng đến quy mô dòng thương mại quốc tế. Theo định luật vạn vật hấp dẫn của Newton (1687), mô hình này phản ánh rằng quy mô thương mại giữa 2 quốc gia tỷ lệ thuận với GDP của các quốc gia và tỷ lệ nghịch với khoảng cách địa lý giữa chúng.

Ban đầu, mô hình trọng lực bị phê phán là thiếu nền tảng lý thuyết. Tuy nhiên, những nghiên cứu sau này đã bổ sung nền tảng lý thuyết và và thực nghiệm cho mô hình (thông qua các biến độc lập mới). Một số biến độc lập mới phổ biến là: GDP bình quân đầu người, tỷ giá hối đoái, độ mở của nền kinh tế, v.v…

Mô hình này cũng đã được sử dụng trong quan hệ quốc tế để đánh giá tác động của các hiệp ước và liên minh đối với thương mại.

Ước lượng kinh tế lượng của phương trình trọng lực

Do mô hình lực hấp dẫn trong thương mại không đúng nên trong các ứng dụng kinh tế lượng người ta thường xác định như sau.

Thực ra mô hình như vầy vẫn chưa chạy được nên sẽ tiến hành logarit hai vế dẫn đến mô hình log-log có dạng (lưu ý: hằng số G trở thành một phần của Bo)

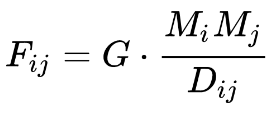
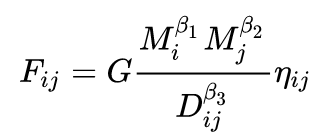
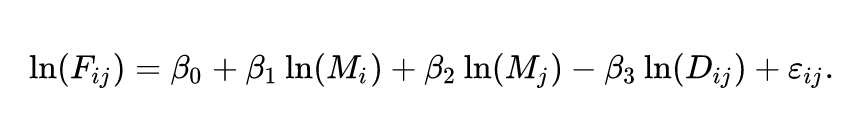
{\displaystyle F_{ij}}đại diện cho khối lượng thương mại từ quốc gia i đến quốc gia j

Mi, Mj thường đại diện cho GDP của các quốc gia  

{\displaystyle D_{ij}}biểu thị khoảng cách giữa hai nước

Mô hình trọng lực thực tế khi làm luận văn

Thực tế khi áp dụng stata để làm luận văn, mô hình có biến phụ thuộc F chính là giá trị export từ 1 quốc gia đến 1 quốc gia.

Biến độc lập là GDP  hai nước, dân số POP hai nước, khoảng cách hai nước….

Ví dụ mô hình trọng lực như sau
ln_exp = b0 + b1*ln_gdpvn + b2*ln_pro + b3*infvn + b4*ln_dis + b5*ln_gdpim +b6*ln_popim +b7*ln_exrim +b8*wto + b9*Border

Biến độc lập

gdpvn : GDP của Việt Nam
pro
inf     : Lạm phát của VN
dis    : Khoảng cách từ VN đến nước đó
gdpim: GDP của nước nhập khẩu hàng từ VN
popim: Dân số của nước nhập khẩu hàng từ VN
exrim
wto   : Có giá nhập WTO chưa
Border: Có biên giới chung với VN không

Biến phụ thuộc
Exp: Giá trị xuất khẩu từ VN đi nước đó

Bảng số liệu mô hình trọng lực:

Sau đó ta tiến hành coding ở Stata để tiến hành chạy dữ liệu bảng cho mô hình trọng lực nhé

Như vậy việc hiểu lý thuyết , mục đích và ứng dụng chạy mô hình trọng lực trong Stata đã xong. Bạn cần hỗ trợ cứ liên hệ nhóm nhé. Zalo 0903396688

 

Hướng dẫn viết câu lệnh Stata trong DO file để xử lý các trường hợp bài phức tạp

Stata

Thực hiện các câu lệnh Stata phức tạp, ví dụ tính trung bình doanh thu từng ngành, hoặc tổng doanh thu từng ngành, hoặc tính phần dư của các mô hình hồi quy theo từng mã chứng khoán… chưa bao giờ là điều đơn giản, vì điều này liên quan kĩ thuật lập trình.

Hôm nay nhóm MBA Hỗ Trợ Stata giới thiệu đến các bạn ví dụ để tạo và thực thi câu lệnh Stata trong môi trường Stata để thực hiện các phân tích thống kê và xử lý dữ liệu phức tạp

Ví dụ về tình huống cần viết câu lệnh Stata vòng lặp

Ví dụ sau ta có số liệu tài chính của các công ty niêm yết trên thị trường.

Phương trình hồi quy như sau:

ROA= b0 + b1*ROA_t_1+residual

Và đề bài đặt ra là: ta cần tìm giá trị b1 và residual ứng với từng mã chứng khoán, thì ta làm như thế nào. Ở đây một mã có 5 năm, nên mỗi phương trình như vậy chỉ có 5 biến quan sát.

Viết câu lệnh Stata vòng lặp để xử lý các trường hợp bài phức tạp

Sau đây là câu lệnh:

xtset MaCK_num Nam
gen ROA_t_1=l.ROA
xtset, clear
 gen phandu=.
 gen beta_ROA_t_1=.

levelsof MaCK_num, local(level)
foreach i of local level {
    display `i'
    regress ROA ROA_t_1  if MaCK_num==`i'
    predict res, residuals
    replace phandu=res if MaCK_num==`i'
    drop res
    display _b[ ROA_t_1 ]
    replace beta_ROA_t_1=_b[ ROA_t_1 ] if MaCK_num==`i'
    }

Các câu lệnh ở trên đã thực hiện vòng lặp theo từng mã chứng khoán , và thực hiện hồi quy. Sau đó lưu phần dư và hệ số beta vào các cột số liệu, kết quả chạy ra được như sau:

Cột phandu và beta_ROA_t_1 chính là 2 cột kết quả ta cần tính.

Ngoài ra có thể áp dụng thêm cách lệnh khác như:

bysort Nganh Nam : egen Doanhthu_nganh=mean (DoanhThuThuan)  để tính trung bình doanh thu từng ngành theo từng năm

egen Std_CFO=sd (CFO), by (MaCK_num)  để tính độ lệch chuẩn của từng mã chứng khoán

Trên đây là ví dụ một số câu lệnh Stata phức tạp. Khi làm bài bạn có cần viết câu lệnh Stata để xử lý tính toán thì cứ liên hệ nhóm nhé

Xử lý lỗi chi2 nhỏ hơn 0 khi kiểm định hausman

Stata

Kiểm định Hausman là gì?

Kiểm định Hausman được sử dụng để so sánh hai phương pháp ước lượng : mô hình tác động ngẫu nhiên (RE) và mô hình tác động cố định (FE). Kiểm định này kiểm tra xem liệu các ước lượng của RE có phù hợp hơn so với FE hay không. Nếu giá trị p của kiểm định Hausman nhỏ hơn mức ý nghĩa thống kê được chọn (thường là 0,05 hoặc 0,01), thì chúng ta sẽ từ chối giả thuyết không rằng RE là phù hợp và chấp nhận giả thuyết thay thế rằng FE là phù hợp hơn.

Lỗi chi2<0  , chi bình phương bé hơn 0 xuất hiện khi nào.

Sau khi chạy kiểm định hausman, nếu giá trị p<5% thì dĩ nhiên ta chọn mô hình FEM mà không chọn REM. Tuy nhiên có trường hợp xuất hiện lỗi sau:

chi2<0 ==> model fitted on these data fails to meet the asymptotic assumptions of the Hausman test; see suest for a generalized test

Như ảnh dưới:

Để xử lý lỗi này, bạn cần hiểu rõ rằng kiểm định Hausman chỉ có thể được sử dụng khi các giả thuyết phân phối của ước lượng RE và FE đều thoả mãn, và khi đó giá trị thống kê của kiểm định là một giá trị không âm của phân phối chi bình phương (chi-square distribution).

Nếu giá trị chi bình phương (chi-square) trong kiểm định Hausman nhỏ hơn 0, điều này có nghĩa là mô hình không đáp ứng được các giả thuyết phân phối và không đáp ứng được tiêu chuẩn của kiểm định. Trong trường hợp này, bạn không thể sử dụng kiểm định Hausman để so sánh giữa ước lượng RE và FE.

Thay vào đó, bạn có thể sử dụng phương pháp suest (Seemingly Unrelated Estimation) để so sánh ước lượng giữa các mô hình RE và FE. Phương pháp này được sử dụng để kết hợp các mô hình ước lượng phức tạp hơn, giúp tăng độ chính xác của các ước lượng và đưa ra các giả định phù hợp hơn. Suest cung cấp một kiểm định tổng quát hơn để so sánh giữa các mô hình, bao gồm cả RE và FE, mà không yêu cầu giả định phân phối như kiểm định Hausman.

Vì vậy, nếu giá trị chi bình phương của kiểm định Hausman nhỏ hơn 0, bạn có thể sử dụng phương pháp suest để so sánh giữa các mô hình ước lượng RE và FE.

Cách xử lý lỗi chi2 <0 , giá trị p không xuất hiện

Có một số cách khắc phục lỗi này:

1. Thay đổi tăng hoặc giảm số lượng quan sát rồi chạy lại cho đến khi ok.

2. Thay đổi thứ tự tham số trong hausman, ví dụ : hausman fixed random thì đổi thành hausman random fixed. Tuy nhiên cách này sẽ ra được giá trị p, và chỉ để tham khảo chứ không kết luận được dựa vào cách này.

Cách gán dữ liệu thời gian dạng hàng quý, hàng tháng cho bộ số liệu theo thời gian với lệnh xtset và tsset

Stata,

Nhóm thạc sĩ Bách Khoa giới thiệu đến các bạn câu lệnh gán số liệu thời gian trong các trường hợp chu kì thời gian là tháng, quý, năm nhé.

Cả lệnh xtset và tsset trong Stata đều được sử dụng để thiết lập biến thời gian cho dữ liệu dạng chuỗi thời gian (time series data). Tuy nhiên, chúng được sử dụng cho các loại dữ liệu khác nhau và có một số khác biệt về cách sử dụng.
– tsset được sử dụng cho các dữ liệu chuỗi thời gian đơn giản, trong đó thời gian được biểu thị bằng một biến duy nhất, ví dụ như dữ liệu thời gian hàng ngày, hàng tuần, hàng tháng hoặc hàng quý. Để sử dụng tsset, bạn cần chỉ định biến thời gian và định dạng thời gian của biến đó.
– xtset được sử dụng cho các dữ liệu panel – dữ liệu bảng – có hai hoặc nhiều biến thời gian, ví dụ như dữ liệu trên thị trường chứng khoán, gồm nhiều công ty, và một công ty có nhiều năm. Trong xtset, cần chỉ định tên biến đại diện cho không gian( ví dụ mã công ty) và biến thời gian.

Gán dữ liệu thời gian dạng hàng quý

Ví dụ: giả sử bạn có tập tin dữ liệu về doanh số bán hàng của một công ty trong 4 quý đầu năm. Các biến trong tập tin dữ liệu bao gồm: quý (QUY) ở dạng 2007q1 2007q2 2007q3 2007q4 2008q1 2008q2 2008q3 2008q4 , và doanh số bán hàng (sales). Để sử dụng lệnh tsset cho dữ liệu này, bạn có thể làm như sau:

gen qdate = quarterly(QUY, "YQ")
format qdate %tq
tsset qdate, quarterly

Gán dữ liệu thời gian dạng hàng tháng

Tháng đang là: Thang: 2009m1,2009m2,…2009m12…

Thì làm như sau:
gen qdate = monthly(Thang, "YM")
format qdate %tm
tsset qdate

Bạn có thể áp dụng các câu lệnh tương tự cho xtset nhé.

Gán dữ liệu thời gian dạng hàng năm

Còn nếu số liệu dạng hàng năm thì quá dễ rồi, câu lệnh như sau:

tsset  YEAR

không cần format, hoặc gen để tạo biến gì cả nhé

Cả xtset và tsset đều có thể được sử dụng để giúp Stata hiểu được cấu trúc dữ liệu của và thực hiện các phân tích liên quan đến chuỗi thời gian hoặc panel data. Chúng là những lệnh quan trọng và hữu ích cho các nhà nghiên cứu và phân tích dữ liệu sử dụng Stata.

Bạn cứ trao đổi thêm với nhóm ở đây, hoặc comment bên dưới nhé.

Liên hệ nhóm thạc sĩ Hỗ trợ Stata.

– SMS, Zalo, Viber:

phone number

– Facebook  facebook.com/hotroStata

– Email  hotrostata@gmail.com

Tải phần mềm Stata 17 miễn phí, cài đặt dễ dàng

Stata

Nhóm Thạc Sĩ hướng dẫn  các bạn tải phần mềm Stata 17 phiên bản 64 bít, cài đặt dễ dàng

Các bạn tải phần mềm Stata miễn phí bảng 17 x64  ở  đây  http://download.phantichspss.com/download/stata/ bằng cách chọn file stata17.zip

Sau đó giải nén ra, bấm vào file Setup.exe để chạy chương trình. Cứ thế nhấn next, ok…

Sau khi cài xong thì chép file StataMP-64.exe trong thư mục Cracked exe đè vào file chương trình đã được cài đặt trong ổ C như sau

Lưu ý bạn phải đảm bảo là đã chép đè file thành công. Nhiều bạn sau khi chép vẫn bị bắt nhập số serial khi mở stata lên, là do chép đè chưa thành công. Một cách an toàn là bạn hãy xóa file StataMP-64.exe trong thư mục Program Files này trước, sau đó copy file StataMP-64.exe trong thư mục Cracked exe vào đây nhé.

Sau đó cứ bật chương trình Stata17 lên và sử dụng enjoy it.

Như vậy việc tải và cài đặt Stata 17 miễn phí đã hoàn tất, các bạn có thể sử dụng nhé. Trong quá trình sử dụng các bạn có cần hỗ trợ cứ liên hệ nhóm theo số phone sau nhé

 

Stata các loại biến, các loại mô hình trong dữ liệu bảng data panel

Stata,

Bốn loại biến cơ bản trong dữ liệu bảng panel data

Có bốn loại biến cơ bản có thể được sử dụng trong mô hình dữ liệu bảng panel data:

  1. Đầu tiên là các biến khác nhau giữa các đơn vị phân tích, nhưng không thay đổi theo thời gian (ví dụ: chủng tộc và giới tính, loại hình công ty hoặc cấp học).
  2. Loại biến thứ hai có thể thay đổi theo thời gian, nhưng giống nhau đối với tất cả các đơn vị phân tích tại bất kỳ khoảng thời gian nhất định nào (ví dụ: các chỉ tiêu kinh tế quốc gia: GDP, lạm phát).
  3. Loại thứ ba là một biến số có thể thay đổi theo cả thời gian và đơn vị phân tích(ví dụ: thu nhập, chi tiêu công ty, thành phần học sinh đi học).
  4. Biến cuối cùng là biến thay đổi theo thời gian theo mô hình có thể dự đoán được (ví dụ: thước đo tuổi hoặc thâm niên,ví dụ năm nay thâm niên 10 năm thì sang năm sau chắc chắn sẽ là 11 năm). Việc bao gồm một số biến, chẳng hạn như những biến thay đổi theo đơn vị nhưng không thay đổi theo thời gian, phụ thuộc vào việc sử dụng các hiệu ứng cố định hay ngẫu nhiên. Những cái khác, chẳng hạn như những cái có yếu tố thời gian sẽ phụ thuộc vào khía cạnh thời gian được diễn giải trong mô hình. Nhưng phân tích dữ liệu bảng có các tùy chọn mà theo đó tất cả các loại biến này có thể được đưa vào một số kiểu như là cố định, ngẫu nhiên….

Các loại mô hình cơ bản trong panel data

Các mô hình dữ liệu bảng panel data có thể được sử dụng cho nhiều loại mô hình, từ đơn giản đến những mô hình có mối quan hệ khá phức tạp. Loại mô hình cơ bản nhất là hồi quy pooled OLS, loại bỏ sự phụ thuộc lẫn nhau giữa các quan sát trong một đơn vị phân tích và ước tính một hệ số chặn và hệ số góc không đổi theo thời gian và đơn vị. Điều này tương đương với việc chạy một mô hình hồi quy cơ bản trong đó biến thời gian bị bỏ qua và tất cả các quan sát được phân tích cùng nhau. Mặc dù mô hình này có vấn đề với việc bỏ qua các phụ thuộc trong cùng 1 đơn vị phân tích( ví dụ 1 công ty), nhưng nó có thể tạo thành một mô hình cơ sở cho các mục đích so sánh. Nhưng ta phải được thận trọng vì các hệ số ước tính có thể cung cấp kết quả sai lệch. Tập hợp các mô hình tiếp theo tập trung vào các mức độ khác nhau của kết quả theo đơn vị phân tích cụ thể, trong đó các hệ số chặn, hệ số hồi quy hoặc cả hai thay đổi theo đơn vị.

Lựa chọn giữa fixed effects và random effects

Sự lựa chọn giữa các hiệu ứng cố định và ngẫu nhiên trong các mô hình bảng chủ yếu tập trung vào sự đánh đổi giữa việc kiểm soát tính nội sinh trong các hiệu ứng cố định với hiệu quả thống kê, nhưng kết quả sai lệch do các tác động ngẫu nhiên. Các tác động cố định cung cấp một cách đơn giản để kiểm soát các biến chưa hoặc không thể đo lường được. Điều này được thực hiện bằng cách phân tích từng đơn vị riêng biệt với các hiệu ứng cố định. Bằng cách này, các biến không quan sát được mà không thay đổi theo thời gian là không đổi trong các khoảng thời gian và do đó không thể có bất kỳ ảnh hưởng nào đến kết quả. Bằng cách sử dụng mỗi đơn vị phân tích cho nó tự kiểm soát riêng và các quan sát có quan hệ các quan sát khác trong nhóm, hầu hết các dạng nội sinh đều bị loại bỏ. Nó không thể giải thích cho các biến không được đo lường thay đổi theo thời gian, nhưng tất cả các dạng khác đều được giải quyết. Hơn nữa, các biến không thay đổi theo đơn vị, chẳng hạn như giới tính, v.v., không thể được phân tích vì chúng không đổi trong khoảng thời gian. Do đó, các hiệu ứng cố định sử dụng sự thay đổi trong nội bộ đơn vị để ước tính tất cả các ảnh hưởng và tăng tính nhất quán với chi phí hiệu quả.

Tuy nhiên, các tác động ngẫu nhiên mang lại một loạt các lợi ích và hạn chế khác nhau. Chúng yêu cầu ít tham số ước tính hơn (chủ yếu bằng cách không ước tính điểm chặn cho mỗi đơn vị) và do đó tăng bậc tự do có sẵn. Ngoài ra, các biến bất biến theo thời gian như giới tính hoặc chủng tộc hiện có thể được đưa vào phân tích. Nhưng tất cả những lợi ích này phải được cân nhắc dựa trên sự sai lệch tiềm năng từ các hiệu ứng nội sinh có thể ảnh hưởng đến các ước tính tác động ngẫu nhiên. Do đó, sự lựa chọn giữa các tác động cố định và ngẫu nhiên là sự đánh đổi giữa việc kiểm soát tính nội sinh so với việc tăng hiệu quả và mở rộng các loại biến.

Tóm lại

Mô hình dữ liệu bảng là một khung phân tích được thiết kế cho một cấu trúc dữ liệu cụ thể ,cross-sectional kết hợp với dữ liệu dọc longitudinal, nói đơn giản là ví dụ có nhiều công ty, mỗi một công ty có nhiều năm , mỗi năm đều có các số liệu của công ty đó thì đó là dữ liệu bảng.

Tác động cố định, ngẫu nhiên, kích cỡ mẫu tối thiểu với data panel

Stata

Bài này sẽ ví dụ về biến cố định và biến ngẫu nhiên trong dữ liệu bảng,đồng thời giới thiệu về cỡ mẫu phù hợp khi chạy dữ liệu bảng Stata

Tác động cố định và tác động ngẫu nhiên

Có lẽ khái niệm xa lạ nhất đối với hầu hết các nhà nghiên cứu sử dụng hồi quy là tác động cố định so với ngẫu nhiên. Một điểm khác biệt chung giữa tác động cố định và tác động ngẫu nhiên là tác động cố định được sử dụng cho các tham số tổng thể (tức là một giá trị cố định duy nhất trên toàn bộ tổng thể) và tác động ngẫu nhiên được sử dụng khi biến chỉ đại diện cho một mẫu các tác động có thể xảy ra. Ví dụ, giới tính của học sinh sẽ được giả định là một ảnh hưởng cố định vì không bao giờ thay đổi. Nhưng thông tin  về các lớp học của học sinh được chọn ngẫu nhiên trong một trường học thì sao? Trong tình huống này, một hiệu ứng ngẫu nhiên đối với lớp sẽ xảy ra, ví dụ 2 học sinh học lớp 5A có giới tính là nam, thì sang lớp 6 cũng có giới tính là nam, tuy nhiên 2 học sinh này khi vào lớp 6 thì có thể 2 em vào lớp 6A và 6B, nghĩa là thông tin về lớp học là ngẫu nhiên không cố định.

Cuối cùng, sự lựa chọn giữa các hiệu ứng cố định và ngẫu nhiên như thế nào? Trong khi nhà nghiên cứu nên xem xét tác động của các tác động cố định so với ngẫu nhiên dựa trên các vấn đề đã thảo luận ở trên, thì cũng có một thử nghiệm thực nghiệm để cung cấp hướng dẫn. Kiểm định Hausman so sánh kết quả của mô hình hiệu ứng cố định với kết quả của mô hình hiệu ứng ngẫu nhiên. Mức ý nghĩa p= 0,05 ủng hộ giả thuyết rằng có sự khác biệt giữa hai mô hình và do đó mô hình tác động cố định nên được sử dụng. Nếu không có sự khác biệt đáng kể thì có thể sử dụng mô hình hiệu ứng ngẫu nhiên vì nó được ưu tiên hơn so với mô hình hiệu ứng cố định.

Cỡ mẫu khi chạy dữ liệu bảng

Cỡ mẫu phụ thuộc vào mức độ và dựa trên số lượng đơn vị phân tích. Như hồi quy OLS đơn giản, tất cả mẫu đều được sử dụng. Nhưng khi chúng ta chuyển sang các cấp phân tích cao hơn, đơn vị phân tích sẽ thay đổi thành số nhóm trên mỗi cấp (ví dụ: số lớp học, không phải số học sinh). Hơn nữa, số lượng quan sát mỗi nhóm ít quan trọng hơn số lượng nhóm. Quy mô nhóm từ năm quan sát trở lên có thể chấp nhận được miễn là  số lượng nhóm đủ lớn. Vậy có bao nhiêu nhóm và bao nhiêu quan sát mỗi nhóm là chấp nhận được? Heck và Thomas đề xuất quy tắc 20/30 — ít nhất 20 nhóm và 30 quan sát mỗi nhóm. Hox thay đổi điều này một chút với quy tắc 30/30 — ít nhất 30 nhóm và 30 quan sát cho mỗi nhóm. Tuy nhiên, nhiều tình huống nghiên cứu sẽ khác nhau, vì vậy điều nào là quan trọng nhất cần xem xét? Theo nghĩa thực tế, đó là số lượng các nhóm ở bất kỳ cấp độ nào, vì các nhóm bây giờ là đơn vị quan sát để phân tích. Tốt hơn là nên có 30 nhóm với 10 quan sát mỗi nhóm  hơn 10 nhóm với 60 quan sát mỗi nhóm vì có nhiều nhóm hơn để ước tính các tham số. Vì vậy, việc tăng số lượng nhóm ở bất kỳ cấp độ nào luôn hữu ích cho việc ước tính các ảnh hưởng ở cấp độ đó và tăng sức mạnh thống kê.

Vậy quy mô một nhóm có thể nhỏ đến mức nào?

Quy mô nhóm năm thành viên gặp phải trong nhiều tình huống nghiên cứu và cung cấp các ước tính hợp lý. Hơn nữa, chúng không ảnh hưởng đến sức mạnh của các bài kiểm định vì điều đó đến từ số lượng nhóm. Nhưng quy mô nhóm nhỏ hơn sẽ hạn chế độ chính xác của các bài kiểm tra hệ số ngẫu nhiên (sự khác biệt giữa các nhóm về các hệ số chặn hoặc các biến độc lập).

Cách import số liệu nhập file excel vào stata

Stata

Nhóm MBA Bách Khoa hướng dẫn bạn cách đưa file excel vào chương trình Stata để thực hiện phân tích số liệu nhé.

Các bước import số liệu nhập file excel vào stata

Bước 1: Mở chương trình Stata

Bước 2: Vào menu File-Import-Excel Spreadsheet

Bước 3: Bấm nút Browse để chọn file excel, sau đó check vào Import first row as variable names.( nếu file excel có nhiều sheet thì bạn nhớ chọn đúng sheet cần đưa vào ở mục Worksheet nhé)

Sau đó nhấn ok. Là dữ liệu đã được đưa vào Stata rồi nhé

Để kiểm tra lại, bạn có thể gõ lệnh sum để thống kê mô tả các biến để xem đưa vào thành công chưa nhé

Như vậy bạn đã biết cách import số liệu nhập file excel vào stata. Quá trình làm có thắc mắc các bạn cứ liên hệ nhóm nhé.

 

Chuyển dạng số liệu từ số liệu dài thành số liệu rộng, long->wide

Stata

Số liệu từ dài sang rộng được minh họa như bên dưới
 
Phần này minh họa sức mạnh và sự đơn giản của Stata trong khả năng định hình lại các file dữ liệu. Những ví dụ này lấy các file số liệu dài và định hình lại chúng thành dạng rộng. Hình minh họa như trên.

Ví dụ 1: reshape 1 biến

Bạn nhập cách lệnh sau vào Stata để tạo bộ số liệu dọc nhé

clear
input famid birth age
1 1 9
1 2 6
1 3 3
2 1 8
2 2 6
2 3 2
3 1 6
3 2 4
3 3 2
end
list
 
Gõ lệnh sau để tạo số liệu ngang

reshape wide age, i ( famid) j (birth)
 

Ví dụ 2: reshape nhiều biến

Bạn nhập cách lệnh sau vào Stata để tạo bộ số liệu nhé

clear
input famid kidname birth age wt sex
1 Beth 1 9 60 f
1 Bob 2 6 40 m
1 Barb 3 3 20 f
2 Andy 1 8 80 m
2 Al 2 6 50 m
2 Ann 3 2 20 f
3 Pete 1 6 60 m
3 Pam 2 4 40 f
3 Phil 3 2 20 m
end
list

Giờ ta sẽ chuyển dữ liệu long về wide như sau
reshape wide kidname age wt sex, i(famid ) j(birth)
list

Và đây là kết quả
 

Ví dụ 3: mã hóa với hậu tố là chuỗi

Nhập lệnh sau để có được số liệu thu nhập của cha và mẹ
clear
input famid str4 name inc str4 dadmom
2 Art 22000 dad
1 Bill 30000 dad
3 Paul 25000 dad
1 Bess 15000 mom
3 Pat 50000 mom
2 Amy 18000 mom
end
list
 
Nhập lệnh sau nhé:

reshape wide name inc, i(famid) j(dadmom) string

Và đây là kết quả

Bạn cứ trao đổi thêm với nhóm ở đây, hoặc comment bên dưới nhé.

Liên hệ nhóm thạc sĩ Hỗ trợ Stata.

– SMS, Zalo, Viber:

phone number

– Facebook  facebook.com/hotroStata

– Email  hotrostata@gmail.com